Formule pour calculer la distribution T de Student
La formule pour calculer la distribution T (qui est également connue sous le nom de distribution T de Student) est représentée par soustraction de la moyenne de la population (moyenne du deuxième échantillon) de la moyenne de l'échantillon (moyenne du premier échantillon) qui est (x̄ - μ) qui est alors divisé par l'écart-type des moyennes qui est initialement divisé par la racine carrée de n qui est le nombre d'unités dans cet échantillon (s ÷ √ (n)).
La distribution T est une sorte de distribution qui ressemble presque à la courbe de distribution normale ou à la courbe en cloche mais avec une queue un peu plus grosse et plus courte. Lorsque la taille de l'échantillon est petite, cette distribution sera utilisée au lieu de la distribution normale.
t = (x̄ - μ) / (s / √n)
Où,
- x̄ est la moyenne de l'échantillon
- μ est la moyenne de la population
- s est l'écart type
- n est la taille de l'échantillon donné
Calcul de la distribution T
Le calcul de la distribution t de Student est assez simple, mais oui, les valeurs sont obligatoires. Par exemple, il faut la moyenne de la population, qui est la moyenne de l'univers, qui n'est rien d'autre que la moyenne de la population alors que la moyenne de l'échantillon est nécessaire pour tester l'authenticité de la population signifie si l'énoncé revendiqué sur la base de la population est bien vrai et l'échantillon, le cas échéant, représentera la même déclaration. Ainsi, la formule de distribution t soustrait ici la moyenne de l'échantillon de la moyenne de la population, puis la divise par l'écart type et les multiples par la racine carrée de la taille de l'échantillon pour normaliser la valeur.
Cependant, comme il n'y a pas de plage pour le calcul de la distribution t, la valeur peut devenir bizarre, et nous ne serons pas en mesure de calculer la probabilité car la distribution t de Student a des limites pour arriver à une valeur, et par conséquent elle n'est utile que pour une taille d'échantillon plus petite . De plus, pour calculer la probabilité après avoir obtenu un score, il faut trouver la valeur de celui-ci à partir de la table de distribution t de l'élève.
Exemples
Exemple 1
Tenez compte des variables suivantes qui vous sont données:
- Moyenne de la population = 310
- Écart type = 50
- Taille de l'échantillon = 16
- Moyenne de l'échantillon = 290
Calculez la valeur de la distribution t.
Solution:
Utilisez les données suivantes pour le calcul de la distribution T.

Ainsi, le calcul de la distribution T peut être effectué comme suit:
Ici toutes les valeurs sont données. Nous avons juste besoin d'incorporer les valeurs.
Nous pouvons utiliser la formule de distribution t

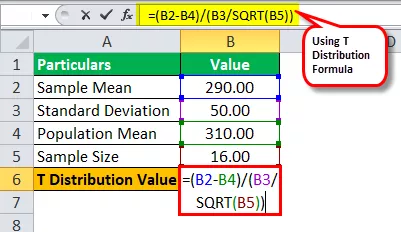
Valeur de t = (290-310) / (50 / √16)

Valeur T = -1,60
Exemple # 2
La société SRH affirme que ses employés au niveau des analystes gagnent en moyenne 500 $ l'heure. Un échantillon de 30 employés au niveau des analystes est sélectionné, et leur salaire horaire moyen était de 450 $, avec un écart d'échantillon de 30 $. Et en supposant que leur affirmation est vraie, calculez la valeur de distribution t, qui sera utilisée pour trouver la probabilité de distribution t.
Solution:
Utilisez les données suivantes pour le calcul de la distribution T.
Ainsi, le calcul de la distribution T peut être effectué comme suit:
Ici toutes les valeurs sont données; nous avons juste besoin d'incorporer les valeurs.
Nous pouvons utiliser la formule de distribution t


Valeur de t = (450 - 500) / (30 / √30)

Valeur T = -9,13
Par conséquent, la valeur du score t est -9,13
Exemple # 3
Universal College Board avait administré un test de niveau de QI à 50 professeurs choisis au hasard. Et le résultat qu'ils ont trouvé à partir de cela était le score moyen de niveau de QI était de 120 avec une variance de 121. Supposons que le score t est de 2,407. Quelle est la moyenne de la population pour ce test, ce qui justifierait la valeur du score t de 2,407?
Solution:
Utilisez les données suivantes pour le calcul de la distribution T.

Ici, toutes les valeurs sont données avec la valeur t; nous devons calculer la moyenne de la population au lieu de la valeur t cette fois.
Encore une fois, nous utiliserons les données disponibles et calculerons les moyennes de population en insérant les valeurs données dans la formule ci-dessous.
La moyenne de l'échantillon est de 120, la moyenne de la population est inconnue, l'écart-type de l'échantillon sera la racine carrée de la variance, qui serait de 11, et la taille de l'échantillon est de 50.
Ainsi, le calcul de la moyenne de la population (μ) peut être effectué comme suit:
Nous pouvons utiliser la formule de distribution t.


Valeur de t = (120 - μ) / (11 / √50)
2,407 = (120 - μ) / (11 / √50)
-μ = -2,407 * (11 / √50) -120
La moyenne de la population (μ) sera -

μ = 116,26
Par conséquent, la valeur de la moyenne de la population sera de 116,26.
Pertinence et utilisation
La distribution T (et les valeurs de scores t associées) est utilisée dans les tests d'hypothèse lorsque l'on a besoin de savoir si l'on doit rejeter ou accepter l'hypothèse nulle.

Dans le graphique ci-dessus, la région centrale sera la zone d'acceptation et la région de queue sera la région de rejet. Dans ce graphique, qui est un test à deux extrémités, le bleu ombré sera la région de rejet. La zone dans la région de queue peut être décrite soit avec les scores t, soit avec les scores z. Prenons un exemple; l'image de gauche représentera une zone dans les queues de cinq pour cent (qui est de 2,5% des deux côtés). Le score z doit être de 1,96 (en prenant la valeur du tableau z), ce qui représente 1,96 écart-type par rapport à la moyenne ou à la moyenne. L'hypothèse nulle peut être rejetée si la valeur du score z est inférieure à la valeur de -1,96 ou si la valeur du score z est supérieure à 1,96.
En général, cette distribution doit être utilisée comme décrit précédemment lorsque l'on a une taille d'échantillon plus petite (généralement moins de 30 ans) ou si l'on ne connaît pas la variance de la population ou l'écart-type de la population. Pour des raisons pratiques (c'est-à-dire dans le monde réel), ce serait toujours le cas. Si la taille de l'échantillon fourni est suffisamment grande, les 2 distributions seront pratiquement similaires.








