Calculateur d'épargne simple - Calculer le montant à l'échéance de l'individu

À propos du calculateur d'économies simple

La formule est comme ci-dessous:

Mathématiquement, il peut être calculé pour des économies simples uniques:

Deuxièmement, si des économies mensuelles simples sont effectuées, le calcul:

Où,

• M est le montant total à la fin de la période d'épargne simple
• I est le montant initial investi
• i est le montant fixe investi à intervalles réguliers
• r est le taux d'intérêt
• F est la fréquence à laquelle les intérêts sont payés
• n est le nombre de périodes pour lesquelles des économies simples doivent être réalisées.

Il existe de nombreuses banques et autres institutions financières qui se font concurrence sur le marché pour attirer les dépôts afin de pouvoir faire plus d'affaires, c'est-à-dire prêter de l'argent à des entreprises ou à des particuliers fortunés. Certaines banques paieraient un taux d'intérêt plus élevé si les dépôts dépassent certaines limites de seuil et sont conservés dans le compte, ou bien ils paieront un taux d'intérêt standard. De plus, il pourrait y avoir une différence dans les fréquences de paiement des intérêts; par exemple, les intérêts pourraient être composés et payés trimestriellement, semestriellement ou annuellement selon la banque. Par conséquent, avec ce calculateur, les particuliers seraient en mesure de déterminer quelle institution financière ils devraient choisir pour investir leur argent en comparant le montant à l'échéance ou le rendement gagné sur leur capital.

Comment calculer des économies simples?

Il faut suivre les étapes ci-dessous pour calculer les économies simples.

Étape # 1 - Déterminez le montant qui serait investi, qu'il s'agisse d'un montant forfaitaire ou d'un investissement périodique, alors la même chose devrait être considérée dans les calculs de taux d'épargne.

Étape # 2 - Déterminez le taux d'intérêt qui est disponible dans les options pour l'individu, et qui serait gagné ou devrait être gagné sur les économies simples.

Étape # 3 - Maintenant, déterminez la période pour laquelle il sera investi, et la plupart le seront à long terme et dépendront du cas par cas.

Étape # 4 - Divisez le taux d'intérêt par le nombre de périodes pendant lesquelles l'intérêt ou l'intérêt d'épargne simple est payé. Par exemple, si le taux payé est de 5% et qu'il paie mensuellement, alors le taux d'intérêt serait de 5% / 12, soit 0,416%.

Étape # 5- Maintenant, utilisez la formule qui a été discutée ci-dessus au point 1) au cas où les économies simples sont faites de façon forfaitaire et utilisez la formule 2) au cas où le montant des économies simples est effectué à intervalles réguliers avec tout montant initial pour toutes les options disponibles .

Étape # 6 - Le chiffre résultant sera le montant à l'échéance qui inclurait également le revenu d'épargne simple et a choisi celui qui a le paiement le plus élevé en termes d'intérêts.

Exemple de calculateur d'épargne simple

M. William est maintenant adulte et est ravi d'ouvrir son premier compte d'épargne. Il a cherché l'institution financière, qui offre un taux d'intérêt élevé, mais il est perplexe car il ne sait pas quelle banque lui offrira le meilleur rendement. Voici les citations que M. William a sélectionnées.

Il veut investir 1 500 $ dans l'un ou l'autre des comptes, et il investira de la façon dont le compte paie les intérêts. Par exemple, si la banque paie semestriellement, le montant sera investi de manière égale à la fin de chaque période et continuera de le faire pendant une période de 10 ans.

Sur la base des informations fournies, vous devez calculer le montant qu'il épargnerait, les intérêts gagnés sur celui-ci et dans quelle banque il devrait investir.

Solution:

On nous donne les détails ci-dessous:

BANQUE I

• I = le montant initial sera nul
• r = taux d'intérêt qui est de 3,00% et trimestriel il sera de 3,00% / 4 qui est de 0,75%
• N = Fréquence qui est ici trimestrielle; donc ce sera 4
• n = nombre d'années d'économies simples à réaliser, soit 10 ans ici.
• i = C'est le montant régulier à investir, soit 1500/4 soit 375 $

Maintenant, nous pouvons utiliser la formule ci-dessous pour calculer le montant à l'échéance.

• = 0 * (1 + 0,75%) ^{10 * 4} + 375 * ((1 + 0,75%) ^{10 * 4} - 1 / 0,75%)
• = 17 417,43

Le montant à l'échéance sera de 17417,43

Les intérêts composés gagnés seraient de 17 417,43 $ - (375 x 40 $ ) = 2 417,43 $.

BANQUE II

• I = le montant initial sera nul
• r = Taux d'intérêt qui est de 3,12% et semestriel il sera de 3,12% / 2 soit 1,56%.
• N = Fréquence qui est semi-annuelle ici, donc ce sera 2
• n = nombre d'années d'économies simples à réaliser, soit 10 ans ici.
• i = C'est le montant régulier à investir, qui est de 1500/2 soit 750 $

Maintenant, nous pouvons utiliser la formule ci-dessous pour calculer le montant à l'échéance.

• = 0 * (1 + 1,56%) ^{10 * 2} + 750 * ((1 + 1,56%) ^{10 * 2} - 1) / 1,56%
• = 17 445,58 $

La valeur à l'échéance sera de 17445,58 $

Les intérêts composés gagnés seraient de 17 445,58 $ - (750 $ * 20) = 2 445,58 $.

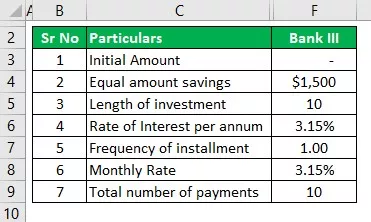
BANQUE III

• I = le montant initial sera nul
• r = taux d'intérêt, qui est de 3,15%, et annuellement, il sera de 3,15% / 1, soit 3,15%
• N = fréquence qui est ici annuellement, donc ce sera 1
• n = nombre d'années d'économies simples à réaliser, soit 10 ans ici.
• i = C'est le montant régulier à investir, soit 1500/1 soit 1500 $

Maintenant, nous pouvons utiliser la formule ci-dessous pour calculer le montant à l'échéance.

• = 0 * (1 + 3,15%) ^{10 * 1} + 1500 * ((1 + 3,15%) ^{10 * 1} - 1) / 3,15%
• = 17315,08 $

Le montant à l'échéance sera de 17315,08 $

L'intérêt composé gagné serait de 17315,08 $ - (1500 $ x 10) = 2315,08 $.

Le montant le plus élevé gagné est dans la banque II, et par conséquent, il devrait ouvrir un compte auprès de la banque II.

Conclusion

Ce calculateur, comme indiqué ci-dessus, peut être utilisé pour comparer les différents montants d'échéance à travers l'institution financière, car un taux d'intérêt plus élevé ne garantit pas le montant absolu le plus élevé, comme le montre l'exemple ci-dessus. Par conséquent, il faut calculer et comparer les montants à travers l'échéance, puis prendre une décision.