Définition de composition
La composition est la méthode de calcul du taux d'intérêt qui est en fait l'intérêt sur les intérêts lorsque les intérêts sont calculés sur l'investissement / le capital initial plus les intérêts gagnés et autres réinvestissements, en d'autres termes, les intérêts gagnés sont accumulés jusqu'au montant du principal en fonction de la période de dépôt ou de prêt. qui peut être mensuel, trimestriel ou annuel
Essayons de comprendre ce qui est composé et comment cela fonctionne à travers quelques exemples de base
Top 4 des exemples de puissance de la composition
Exemple 1
Shane et Mark ont tous deux décidé d'investir 1 00 000 $, mais Shane a décidé d'investir dans des intérêts simples, tandis que Mark investit dans des intérêts composés pendant dix ans à 10% d'intérêt. Voyons ce qui se passe après dix ans.
Solution:
Ainsi, le calcul de l'investissement Shane sera -

Montant total des gains = 200 000 $
Avec un intérêt simple, Shane recevra 2,00 000 $ après 10 ans.
Le calcul de l'investissement en marque sera -

Montant total des gains = 2,59,374 $
Avec l'intérêt composé, la valeur des placements de Mark passera à 2,59 374 $.
Maintenant, Shane a décidé d'investir par des méthodes de composition comme Mark, et ils ont tous deux investi 2,00 000 $ au taux de 15%.
Le calcul de l'investissement Shane sera -

Montant total des gains = 8,09111,55 $
Shane reste investi pendant 10 ans et obtient le montant final de 8,09 111,55 $ au taux de 15%.
Le calcul de l'investissement en marque sera -

Montant total des gains = 65,83,790,52 $
Cependant, Mark fait preuve de patience dans les investisseurs à long terme et reste investi pendant 25 ans, et la valeur de son investissement passe à 65,83,790,52 $.
L'exemple ci-dessus montre la puissance de la composition. Plus l'horizon d'investissement est long, plus la croissance exponentielle est grande.
Exemple # 2 (hebdomadaire)
Simon a 7 500 $ d'économies, et pour le fonds universitaire de son fils, qui va fréquenter l'université après 15 ans, il a décidé d'investir dans des obligations d'épargne américaines. L'objectif de Simon est d'économiser 20 000 $, et le taux annuel en pourcentage d'une obligation d'épargne américaine est de 6%. Quelle est la valeur future de Simon Money après 15 ans?
Solution:
Donné,
- Principal = 7500 $
- Taux = 6% ou 0,06
- Période de temps = 15 ans.
- Combien de fois il est composé en un an n = 52 semaines
- Valeur future =?
Ainsi, le calcul de la valeur future sera -

La formule de composition hebdomadaire est la suivante.
F = P (1 + r / n) n * t- F = 7500 USD (1 + 0,06 / 52) 52 * 15
- F = 7500 USD (1 + 0,001153846) 780
- F = 18 437,45 $
Donc, à partir du calcul ci-dessus, il est clair que l'objectif de Simon d'économiser 20,00 $ ne sera pas atteint avec les méthodes ci-dessus, mais c'est plus proche de cela.
Méthode de composition continue
Essayons maintenant l'exemple ci-dessus avec la formule de composition continue.
Ainsi, le calcul de la valeur future sera -

- F = 7500e $ 0,06 * 15
- F = 7500 $ 0,9
- Valeur future (F) = 18447,02 $
Maintenant, même avec la composition continue, l'objectif de Simon d'économiser 20 000 $ pour le fonds universitaire de son fils ne sera pas atteint.
Voyons avec la formule mensuelle composée que combien d'argent Simon a-t-il besoin d'investir pour atteindre son objectif d'économiser 20 000 $ en 15 ans avec un TAP de 6%?
Ainsi, le calcul de la valeur future sera -
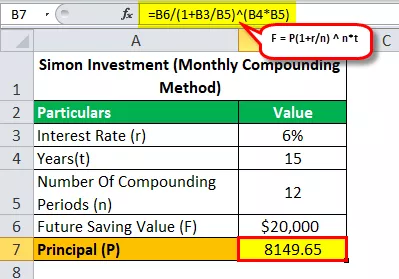
- 20000 USD = P (1 + 0,06 / 12) 12 * 15
- P = 20 000 USD / (1 + 0,06 / 12) 12 * 15
- Principal (P) = 8149,65
Donc, en résolvant l'équation ci-dessus, nous obtiendrons une réponse de 8 149,65 $ (montant que Simon doit investir pour atteindre son objectif d'économiser 20 000 $ en 15 ans).
Exemple n ° 3 (rendement annualisé effectif)
Disons que la banque limitée XYZ donne 10% par an aux seniors pour le dépôt fixe, et nous supposons ici que les intérêts bancaires sont composés trimestriellement comme toutes les autres banques. Calculez le rendement annualisé effectif pour 5, 7 et 10 ans.
Solution:
Rendement annualisé pendant 5 ans:
- t = 5 ans
- n = 4 (trimestriel composé)
- I = 10% par an
Donc A = (1 + 10% / 100/4) (5 * 4)
- A = (1 + 0,025) 20
- A = 1,6386
- I = 0,6386 dans 5 ans
Intérêt effectif = 0,6386 / 5
I effectif = 12,772% par an
Rendement annualisé pendant 7 ans:
- t = 7 ans
- n = 4 (trimestriel composé)
- I = 10% par an
Donc A = (1 + 10% / 100/4) (7 * 4)
- A = (1 + 0,025) 28
- A = 1,9965
- I = 1,9965 dans 7 ans
- I effectif = 0,9965 / 7
I effectif = 14,236% par an
Rendement annualisé pendant 10 ans:
- t = 10 ans
- n = 4 (trimestriel composé)
- I = 10% par an
Donc A = (1 + 10% / 100/4) (10 * 4)
- A = (1 + 0,025) 40
- A = 2,685
- I = 1,685 dans 10 ans
- I effectif = 1,685 / 10
I effectif = 16,85% par an
Exemple # 4 - (Rentes: valeur future)
1 000 $ sont investis tous les 3 mois à 4,8% par an, composés trimestriellement. Combien vaudra la rente dans 10 ans?
Solution:
Donc, quand nous disons combien vaudra la rente dans 10 ans, cela signifie ici que nous devons trouver la valeur future, et c'est important parce que chaque fois qu'il y a un exemple sur les rentes, nous devons voir ce que nous devons découvrir.
Ainsi, la formule de la valeur future est
VF de la rente = P ((1+ r) n - 1 / r)- P = paiement périodique
- r = Tarif par période
- n = nombre de périodes
La formule de la valeur future est donc
- Alors ici P = 1000 $
- r = 4,8% par an ou 0,048
- r (trimestriel) = 0,048 / 4
- r (trimestriel) = 0,012
- n = 10 ans
- n (nombre de fois où la composition s'appliquera) = 10 × 4 = 40
Ainsi, le calcul de la VF de la rente sera -

Alors maintenant FV = 1000 $ (1 + 0,012) 40 -1 / 0,012)
Donc, en résolvant l'équation ci-dessus, vous obtiendrez un FV de 50955,30 $
Alors, combien sera la rente dans 10 ans et la réponse est 50955,30 $
De plus, nous pouvons également découvrir à partir de l'exemple ci-dessus le montant des intérêts gagnés en 10 ans.
Comme 40 fois 1000 $ sont investis, c'est un investissement total (40 × 1000 $ = 40 000 $).
Donc, intérêt = valeur future - investissement total
- Intérêts = 50955,30 $ - 40000 $
- Intérêts = 10955,30 $
Donc ici, il est important de comprendre que dans les rentes, les investisseurs peuvent gagner beaucoup d'intérêts. Dans les exemples particuliers ci-dessus, un dépôt de 40 000 $ donne en retour un intérêt total de 10 955,30 $.
Remarque: vous pouvez télécharger le modèle Excel fourni ci-dessus pour un calcul détaillé.








