Quel est le coefficient de corrélation?
Le coefficient de corrélation est utilisé pour déterminer la force de la relation entre deux variables et ses valeurs peuvent aller de -1,0 à 1,0, où -1,0 représente une corrélation négative et +1,0 représente une relation positive. Il considère les mouvements relatifs dans les variables et définit ensuite s'il existe une relation entre elles.
Formule du coefficient de corrélation
r = n (∑xy) - ∑x ∑y / √ (n * (∑x 2 - (∑x) 2 )) * (n * (∑y 2 - (∑y) 2 ))
Où
- r = coefficient de corrélation
- n = nombre d'observations
- x = 1ère variable dans le contexte
- y = 2 ème variable
Explication
S'il y a une corrélation ou disons la relation entre deux variables, alors cela indiquera si l'une des variables change de valeur, alors l'autre variable aura également tendance à changer de valeur, disons en spécifique qui pourrait être soit la même soit en la direction opposée. La partie numérateur de l'équation effectue un test et la force relative des variables se déplaçant ensemble, et la partie dénominateur de l'équation met à l'échelle le numérateur en multipliant les différences des variables à partir des variables au carré.
Exemples
Exemple 1
Considérez les deux variables suivantes, x et y, vous devez calculer le coefficient de corrélation.
Vous trouverez ci-dessous des données pour le calcul.

Solution:
En utilisant l'équation ci-dessus, nous pouvons calculer ce qui suit

Nous avons toutes les valeurs du tableau ci-dessus avec n = 4.
Entrons maintenant les valeurs pour le calcul du coefficient de corrélation.

Par conséquent, le calcul est le suivant,

r = (4 * 25032,24) - (262,55 * 317,31) / √ ((4 * 20 855,74) - (262,55) 2 ) * ((4 * 30058,55) - (317,31) 2 )
r = 16 820,21 / 16 831,57
Le coefficient sera -

Coefficient = 0,99932640
Exemple # 2
Le pays X est un pays à économie en croissance, et il souhaite mener une analyse indépendante des décisions prises par sa banque centrale concernant les variations des taux d'intérêt, si celles-ci ont eu un impact sur l'inflation et permettent à la banque centrale de les contrôler.
Vous trouverez ci-dessous le résumé du taux d'intérêt et du taux d'inflation qui prévalait dans le pays en moyenne pour ces années.
Vous trouverez ci-dessous des données pour le calcul.

Le président du pays vous a approché pour effectuer une analyse et faire une présentation à ce sujet lors de la prochaine réunion. Utilisez la corrélation et déterminez si la banque centrale a atteint son objectif ou non.
Solution:
En utilisant la formule discutée ci-dessus, nous pouvons calculer le coefficient de corrélation. Traiter le taux d'intérêt comme une variable, disons x, et traiter le taux d'inflation comme une autre variable comme y.

Nous avons toutes les valeurs du tableau ci-dessus avec n = 6.
Entrons maintenant les valeurs pour le calcul du coefficient de corrélation.


r = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
r = -5,36 / 5,88
La corrélation sera -

Corrélation = -0,92
Analyse: Il apparaît que la corrélation entre le taux d'intérêt et le taux d'inflation est négative, ce qui semble être la bonne relation. Au fur et à mesure que le taux d'intérêt augmente, l'inflation diminue, ce qui signifie qu'elles ont tendance à évoluer dans la direction opposée l'une de l'autre, et il ressort du résultat ci-dessus que la banque centrale a réussi à mettre en œuvre la décision relative à la politique des taux d'intérêt.
Exemple # 3
Le laboratoire ABC mène des recherches sur la taille et l'âge et a voulu savoir s'il existe une relation entre eux. Ils ont rassemblé un échantillon de 1000 personnes pour chacune des catégories et ont trouvé une taille moyenne dans ce groupe.
Vous trouverez ci-dessous des données pour le calcul du coefficient de corrélation.

Vous devez calculer le coefficient de corrélation et arriver à la conclusion que s'il existe une relation.
Solution:
Traiter l'âge comme une variable, disons x, et traiter la taille (en cm) comme une autre variable comme y.

Nous avons toutes les valeurs du tableau ci-dessus avec n = 6.
Entrons maintenant les valeurs pour le calcul du coefficient de corrélation.

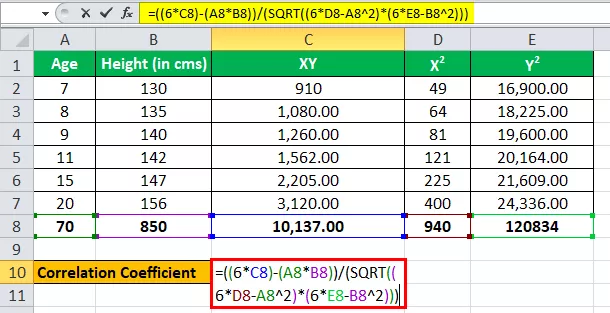
r = (6 * 10 137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1,20 834) - (850) 2 )
r = 1 322,00 / 1 361,23
La corrélation sera -

Corrélation = 0,971177099
Pertinence et utilisation
Il est utilisé dans les statistiques principalement pour analyser la force de la relation entre les variables considérées et en outre, il mesure également s'il existe une relation linéaire entre les ensembles de données donnés et dans quelle mesure ils pourraient être liés. L'une des mesures courantes utilisées pour la corrélation est le coefficient de corrélation de Pearson.
Si une variable change de valeur et avec cette autre variable change de valeur, il est essentiel de comprendre cette relation car on peut utiliser la valeur de la première variable pour prédire le changement de la valeur de la dernière variable. Une corrélation a de nombreux usages multiples aujourd'hui à cette ère moderne, comme elle est utilisée dans le secteur financier, la recherche scientifique et ailleurs. Mais cependant, il est important de savoir que la corrélation a trois grands types de relations. Le premier est une relation positive, qui indique s'il y a un changement dans la valeur d'une variable, alors il y aura un changement dans la variable associée dans la même direction. De même, s'il existe une relation négative, la variable associée se comportera dans la direction opposée. De plus, s'il n'y a pas de corrélation, alors r impliquera une valeur nulle.Voir les images ci-dessous pour mieux comprendre le concept.









