Qu'est-ce que la durée modifiée?
La durée modifiée indique à l'investisseur dans quelle mesure le prix de l'obligation changera, compte tenu de la variation de son rendement. Comme le monde obligataire est plus complexe que le monde boursier, il est important pour l'investisseur de connaître la durée modifiée de l'obligation. Pour simplement calculer d'abord la durée modifiée de l'obligation, l'investisseur doit calculer une dernière chose, qui est la durée de Macauley. Afin de calculer la durée de Macauley, l'investisseur doit déterminer quel est le moment du flux de trésorerie
Formule de durée modifiée
La formule de la durée modifiée est donc simple.
Durée modifiée = Durée Maculay / (1 + YTM / n)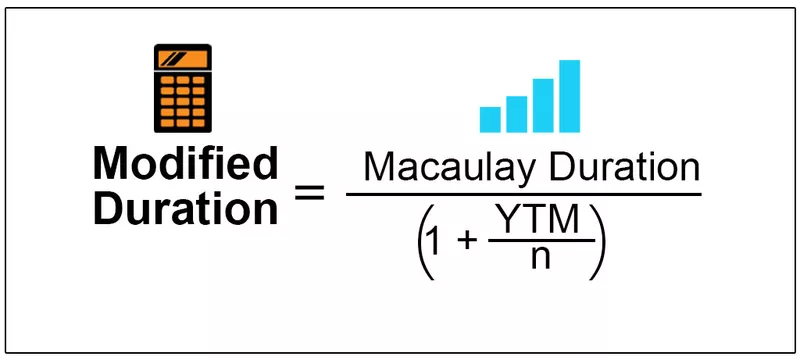
Où,
- Macauley Duration = La duration calcule le temps moyen pondéré avant que l'obligation ne reçoive les flux de trésorerie de l'obligation. La durée modifiée doit être calculée en premier. L'investisseur doit calculer la durée de Macauley de l'obligation.
- YTM = Le rendement à l'échéance est simplement le rendement total que l'investisseur gagnerait dans une obligation lorsque l'obligation est détenue jusqu'à l'échéance
- N = nombre de périodes de coupon par an
Calcul de la durée modifiée avec des exemples
Exemple 1
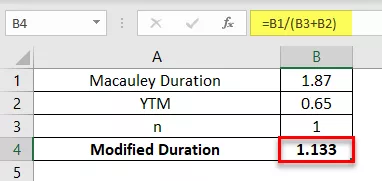
Un paiement annuel de 2 ans d'obligations de 5 000 $ a une durée Macaulay de 1,87 an. Le YTM de l'obligation est de 6,5%. Calculez la durée modifiée de l'obligation.
Exemple # 2
Un paiement annuel de 2 ans d'obligations de 2 000 $ a une durée Macaulay de 2 ans. Le YTM de l'obligation est de 5%. Calculez la durée modifiée de l'obligation.

Exemple # 3
Un paiement annuel de 4 ans d'obligations de 12 000 $ a une durée Macaulay de 5,87 ans. Le YTM de l'obligation est de 4,5%. Calculez la durée modifiée de l'obligation.

Exemple # 4
Un paiement annuel de 5 ans d'obligations de 11 000 $ a une durée Macaulay de 1,5 an. Le YTM de l'obligation est de 7%. Calculez la durée modifiée de l'obligation.

Avantages
- Le principal avantage est que l'investisseur doit connaître la durée de l'obligation car la volatilité des prix des obligations est directement liée aux prix des obligations. Plus la durée de l'obligation est élevée, plus la volatilité des prix est élevée
- La durée de tout instrument d'investissement peut aider à gérer de meilleurs besoins d'investissement pour l'avenir, car l'investisseur peut planifier efficacement le cours futur de son investissement dans la durée
- C'est aussi une mesure du risque de l'obligation au changement et du rendement du prix de l'obligation
- La durée moyenne du fonds est également importante car elle vous indique dans quelle mesure le fonds sera sensible aux variations des taux d'intérêt du marché.
Désavantages
- Le calcul de la durée modifiée est de nature complexe en raison du calcul de la durée de Macaulay, puis l'utilisateur ou l'investisseur a également besoin des entrées de rendement et de durée du calcul de la durée modifiée.
- Il est difficile d'obtenir des données précises et qui prévalent sur le marché car les fluctuations de prix et les prix du marché changent à chaque minute, ce qui rend le calcul incorrect et obsolète.
- La duration n'est pas non plus une mesure complète du risque contenu dans le prix de l'obligation et la durée de l'obligation. L'investisseur ne peut pas se fier seul à la mesure de la durée pour produire des mesures de risque précises
- La duration de Macaulay calcule la duration moyenne pondérée de l'obligation, qui n'est pas à chaque fois une bonne mesure du risque de l'obligation
Conclusion
Modified et Macaulay, bien qu'ayant des limites, est en effet un concept très utile, en particulier pour que les gestionnaires de portefeuille mesurent la volatilité de l'obligation et le risque qui lui est associé, il peut donc servir d'outil très utile lorsque le gestionnaire construit un portefeuille d'obligations et gérer le risque qui y est associé.








